To understand the electric force, gravity and magnetism, we must return to our definition of the aether, because it’s the aether that makes action at a distance possible.
We have to keep in mind that the aether is so dense that every particle in it is in physical contact with every neighbouring particle. This means that if we can manipulate the aether between two surfaces in such a way that some of its particles leave this field, we get tension, forcing the surfaces together. Conversely, if we can manipulate the aether in such a way that particles get sucked into this field, there will be pressure, forcing the surfaces apart. Unless we re-establish equilibrium, there will be tension or pressure, depending on the situation.
Let us further consider what we have said about textures of particles, and the fact that neutrinos are of mixed texture. Neutrinos receive footprints of whatever surface they were last in contact with. This is information that neutrinos take with them as they return back into the field.
Now, consider what happens when a neutrino with a woolly footprint comes in contact with a neutrino with an abrasive footprint. There is a degree of affinity between the two neutrinos. They latch onto each other.
On the other hand, if two neutrinos of identical texture collide, there is virtually no affinity. This means that collisions between equally charged neutrinos are different from collisions of differently charged neutrinos. From this, we can make the following claim based on observation:
Neutrinos of opposite charge collide in such a way that they have a tendency to leave the field, and neutrinos of identical charge collide in such a way that they have a tendency to stay in the field.
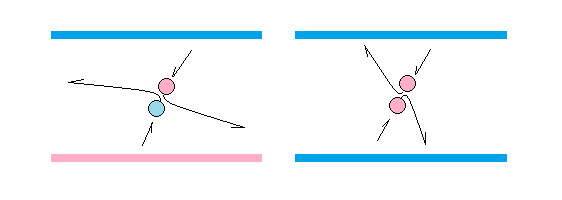
Surfaces of opposite charge attract each other, and surfaces of same charge repel each other, because neutrinos in the aether tend to vacate the field when differently charged, and accumulate when equally charged.
A consequence of this is that there must be electric pressure inside electrons and protons. The walls inside electrons are predominantly negatively charged, and the walls inside protons are predominantly positively charged. In both cases we have a situation in which neutrinos will tend to stay inside. This makes electrons and protons inflated and bouncy, as required for the bouncing electron hypothesis.
On a final note, the relationship between the aether and space must not be forgotten. Space is an aether filled void. When we manipulate the aether, we are manipulating space itself.
Coulomb’s law as availability, probability and geometry
Let us now consider Coulomb’s law to see if we can arrive at this by applying what we have discussed so far.
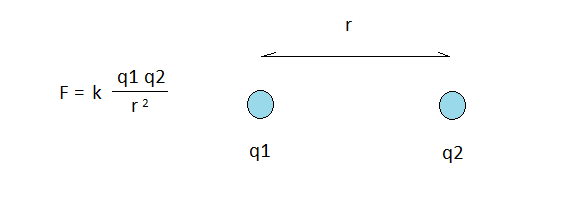
Coulomb’s law states that the force of attraction or repulsion between two point charges, q1 and q2, can be calculated from the strength of the charges themselves, the distance separating them, r, and a constant k. The formula states that the force F equals k multiplied by the product of q1 and q2, divided by the square of r.
This can be related to our theory as follows:
- Let k represent the general availability of neutrinos in the aether.
- Let q1 and q2 represent the probability of collisions between charged neutrinos.
- Let r represent the diminishing chance of collisions with distance.
While point 1 requires no further explanation, we need to explain point 2 and 3. It isn’t immediately clear why q1 should be multiplied by q2, nor why r should be squared.
When it comes to q1 and q2, we have to keep in mind that footprints left on neutrinos are directly related to the charge on the point charges. Q1 and q2 are proxy values for how full the aether is of charged neutrinos.
Furthermore, we have to recognize that collisions are probabilistic events. Such events are calculated using multiplication. When we are talking about very large numbers of collisions, the way we calculate the grand total is also by multiplication. Q1 must therefore be multiplied by q2 in order to give us a value reflecting the overall number of collisions.
When it comes to the distance r, we have to recognize that charged neutrinos are more densely distributed close to the point charges, and that this distribution tapers off by the square of the distance. This is the inverse square law, which can be derived directly from geometry.
From this, we can now calculate the overall number of neutrino collisions by multiplying k with the product of q1 and q2, divided by the square of r. Keeping in mind that it is neutrino collisions that produce force by pumping aether into or out of the field between charges, we have arrived at Coulomb’s law:

From this it’s clear that it’s possible to see Coulomb’s law as an expression related to the aether and the probability of collisions happening in it.
We can also conclude that Coulomb’s law must break down at extremely short distances. This is because this law relates to collisions in the aether. When the distance between two point charges goes to zero, the number of neutrinos between them go to zero as well.
This explains why electrons are only loosely attracted to atomic nuclei when they are in physical contact. With no aether to provide an electric force between the two particles, there’s only their respective textures that keep them together.
The electric force at the surface of a charged particle isn’t infinite nor close to infinite. It’s zero. Very close to the surface it’s near zero. Peak strength of the electric force is at some distance, and we have to move beyond this point for the force to behave fully according to Coulomb’s law.
Electric conditions in and around the atomic nucleus
Having concluded that the electric force falls to zero in the immediate vicinity of charged particles, we can further conclude that there’s no need for a nuclear strong force to keep atomic nuclei from falling apart. All that’s required is the short range weak force that we have modelled as texture.
When we pair this with Morton Spears’ simple model of the proton, it becomes even more apparent that there’s no need for anything beyond this short range weak force. We need only consider the electric conditions in and around the atomic nucleus to see why this is so.
Morton Spears models the proton as an assembly of 2177 positive and negative particle quanta. 1089 are positive and 1088 are negative. The difference of one positive charge constitutes less than 0.05% of the total number of charged particles. This means that from up close, the proton appears to be nearly neutral. There’s close to equal distribution of positive and negative quanta. We have to move away from the proton in order for the overall charge of plus 1 to be registered.
This is in contrast to the electron, which is an assembly of 1 positive and 2 negative charges. This means that an electron attached to a proton will appear from up close as a highly charged negative point on a vast and largely neutral surface.

This means that the electron can perform two different functions inside the atomic nucleus. The electron can stick to protons due to the short range effect of texture, and it can draw protons towards it due to the electric force.
Having already concluded that the neutron is a proton with an electron attached to it, we can now use a proton-electron model of atomic nuclei to explain how they hang together despite having an overall positive charge.
The proton-electron model of the atomic nucleus uses no neutrons. Instead of neutrons it uses protons with an electron stuck to them, and we get assemblies like the ones illustrated below:
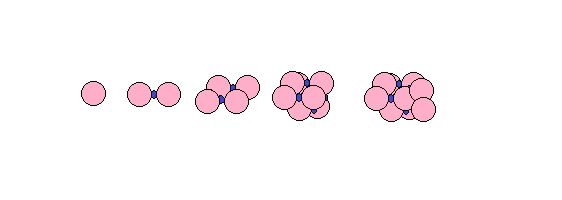
Deuterium is a simple assembly in which two protons are held together by a single electron. The mechanism here is the short range force that we’ve been modelling as texture.
Helium is an assembly of two deuterium nuclei kept together by the electric force. The electron in each deuterium nucleus draws on the protons of their adjacent deuterium nucleus. The helium nucleus is in this way kept together by a combination of texture and the electric force.
Larger nuclei are similarly held together by a combination of texture and electric force.
Note that two deuterium nuclei will repel each other from a distance. They have to get close enough for the electric force of the protons to fade towards zero in order to form helium atoms. This is the challenge scientists have wrestled with for decades in their quest for controlled nuclear fusion.
Note also that we have an explanation for why tritium is a rare and radioactive particle while helium-3 is a stable isotope of helium. The extra electron in the tritium assembly is ejected due to electric repulsion between electrons, and we’re left with the stable configuration of a deuterium nucleus and a proton drawn onto it by the single remaining electron.
We also have an explanation for why the tetraneutron is extremely short lived. Electrons eject other electrons from nuclear assemblies if there are too many of them. There’s strong electric repulsion between electrons inside the nucleus, and at the same time little electric repulsion between protons.
Morton Spears model of the proton makes it possible to imagine two protons sticking together without an electron. Negative patches on one proton connects with positive patches on the other, and visa versa. However, this never happens. The electric repulsion between protons is weak, but not as weak as the short range force we’ve modelled as texture.
On a final note, we can point out that both the nuclear strong force and the nuclear weak force are explained by this model. They are both manifestations of particle texture.
< Electron orbits ———— | ———— Gravity >