Magnetism, the Electric Force and the Speed of Light

When I developed the theory of physics presented here, I came to the conclusion that space must be filled with an aether consisting of low energy photons and neutrinos. All moving at the speed of light. These particles, which I call zero-point neutrinos and zero-point photons, cannot be directly detected due to their low energy. But their existence can explain magnetism as well as the electric force and gravity.

For this reason alone, aether physics has merit.

Remarkable phenomenon

However, there’s a remarkable phenomenon that I’ve skipped lightly over even though it seems to support my theory. Namely the relationship between magnetism, the electric force and the speed of light.

The formula for this is:

• c0 = 1/√(μ0 ε0)
• where c0 is the speed of light in a vacuum, μ0 is vacuum permeability, and ε0 is vacuum permittivity.

The remarkable thing here is that we can calculate the speed of light from two seemingly unrelated values. One relating to magnetism and the other relating to the electric force.

A two component aether

This fits well with our model of the aether. Because it’s a mix of photons and neutrinos, where photons relate to magnetism and neutrinos relate to the electric force, and the speed of light is in turn related to the aether.

The above formula seems to be saying exactly this.

However, I haven’t been able to translate this formula into a simple story. So, I’ve skipped it in my latest books.

Two sided problem

The problem has two sides to it.

First, we have to understand what μ0 and ε0 represent, and how they relate to our model of the aether.

Second, we have to come up with a straight forward story to explain why these values relate to the speed of light in the way they do.

Without a clear understanding of μ0 and ε0 we can obviously not explain their relationship, so we start with these variables to see what we can make of them.

Understanding μ0

First, there’s μ0 which denotes vacuum permeability. It relates the drag that a charged particle experiences when it moves through empty space to the magnetic force it generates.

The relevant illustration is as follows:

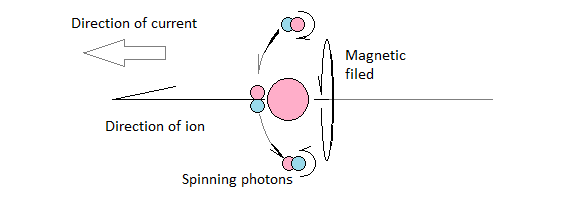
We have a positive ion moving from right to left, which sets photons in the aether spinning, thereby creating the circular magnetic field associated with electric charge in motion.

Moving ions lose momentum due to μ0, which is precisely what we should expect. Because ions transfer some of their momentum onto nearby photons when they move through the aether. This cannot happen without some loss to the ions.

However, the loss is not a constant. It depends on the availability of photons in the aether. The more photons there is in the aether, the more magnetism can be generated with a minimum of effort. So, μ0 goes down when the number of photons go up.

Understanding ε0

Second, there’s ε0 which denotes vacuum permittivity. It tells us how strong an electric field must be in order to produce an electric current through empty space.

The fact that an electric current can pass through empty space is remarkable, and indicative of an aether.

The explanation we have for this is that a strong electric field will produce electron-positron pairs by tearing apart zero-point photons in the aether.

This allows for motion. Electrons move towards the positive side of the field, and positrons move the opposite way, causing a current to flow through space.

However, positrons are unstable. They react with just about anything.

Especially violent reactions occurs when positrons meets electrons. Such collisions result in gamma-ray radiation.

So, currents produced by strong electric fields are associated with high energy radiation.

The fact that ε0 is a finite number suggests that space is a dielectric that functions in the same way that regular dielectric materials function in capacitors. This makes ε0 a threshold value. When an electric field is stronger than this threshold, space becomes a conductor, no longer capable of keeping currents from flowing.

How c0 relates to μ0 and ε0

From this, we see that μ0 and ε0 are both relatively easy to explain in terms of an aether of neutrinos and photons. The problem is not what these two values represent. But why they relate to c0.

The formula c0 = 1/√(μ0 ε0) tells us that c0 can be calculated by multiplying aether drag (μ0) with the aether’s permittivity as a dielectric (ε0). The square root of this multiplication can be inverted to give us the result.

The only difference between detectable and zero-point photons is that detectable ones carry more energy. They are therefore just as susceptible to electric fields as are the photons in the aether. They too can be ripped apart by a strong electric field.

Photons can also be polarized by the Faraday Effect. They may even experience drag as suggested in the tired light hypothesis.

This tells us that light is influenced both by magnetism, represented by μ0, and the electric force, represented by ε0. So, it’s not a complete mystery that the speed of light is dependent on these two factors.

Another thing to note is that permittivity (ε0) is a threshold value. Electric fields in empty space cannot be stronger than this threshold without causing a current to flow. The speed of light (c0) is likewise a threshold. Nothing can move faster than light.

Coulomb’s law

A big clue in all of this is that Coulomb’s law involves a constant k, which is defined as 1/(4 π ε0).

In our aether physics, k represents availability of neutrinos, which means that ε0 represents a lack of neutrinos.

The more neutrinos there is in the aether, the lower the value for ε0.

This makes sense in that a high value for ε0 would correspond to a situation where space is a better dielectric.

If the electric force is communicated by neutrinos, a lack of them would make it harder to rip apart photons. An aether with few neutrinos would be a superior dielectric to an aether with many neutrinos.

Similarly, an increased number of photons in the aether would result in a stronger magnetic force for the same amount of drag.

How photons and neutrinos relate to μ0 and ε0

We can in other words associate μ0 and ε0 with photons and neutrinos in the aether. An increase in photons would make μ0 smaller. An increase in neutrinos would make ε0 smaller.

When we add to this that the aether cannot have an increase in photons and neutrinos at the same time, we see the contours of the formula for c0.

In regions of space where the aether is rich in photons, there’s a corresponding lack of neutrinos, and visa versa.

So, the product of μ0 and ε0 can be expected to remain constant regardless of the aether’s composition.

Photons, neutrinos and clocks

To measure the speed of light, we need clocks. But clocks are affected by the composition of the aether. In regions of space, rich in zero-point neutrinos, clocks go slower than in regions with fewer neutrinos.

This is because the electron and proton depend on neutrinos for their size. Where there’s a lot of neutrinos, electrons and protons are larger. So, energy transfers take more time. Everything is slower, including chemical, nuclear and biological processes. Clocks, being made up of protons and electrons, are no exception.

This means that there is a relationship between the composition of the aether, and physically measured time.

Note also that an increase in zero-point photons results in a decrease in zero-point neutrinos, and visa versa. This is because the aether must be complete no matter what. If there’s a deficiency in photons, there must be a corresponding excess of neutrinos.

So, the effect of an increase in neutrinos is identical to the the effect caused by a decrease in photons.

Tying factors together

This gives us a number of factors that relate to μ0, ε0 and the behavior of clocks. It ties up with our model of the aether as follows:

• An increase in zero-point photons makes:
  • μ0 smaller
  • ε0 bigger
  • magnetic drag weaker
  • space a worse conductor
  • the electric force weaker
  • electrons and protons smaller
  • clocks run faster
• An increase in zero-point neutrinos makes:
  • μ0 bigger
  • ε0 smaller
  • magnetic drag stronger
  • space a better conductor
  • the electric force stronger
  • electrons and protons larger
  • clocks run slower

The aether’s two components act as complete opposites.

Exponential effects

Returning to the formula c0 = 1/√(μ0 ε0), we now see how the above mentioned opposites fit. But only if μ0 and ε0 are exponentials. Because a linear relationship between the two would result in a variable value for c0.

This means that a linear change in quantities of zero-point particles in the aether results in exponential changes to μ0 and ε0.

Figuring out the mechanism behind this is probably key to figuring out why the overall formula has the form that it has.

Curved surfaces and straight lines

Another consideration that may help us explain the formula for c0, is that things at the subatomic are dominated by straight lines of motion and curved surfaces of particles.

This insight led to a straight forward explanation for the mass energy equivalence formula E = mc². So, it may also be key to understand the formula at hand.

For instance, a square root converts a two dimensional surface into a one dimensional straight line.

So, if μ0 times ε0 is related to the surface of particles, the square root of it is a straight line. The total formula for c0 comes in this way across as a transformation of surface areas to straight line paths.

Conclusion

There are plenty of hints buried in the formula c0 = 1/√(μ0 ε0), all pointing to an aether made up of two components.

However, as of yet, I’ve been unable to find a comprehensive explanation for why it has the form that it has.